Algebra 2- Hinweise für die Lehrperson
Achten Sie darauf, dass die Videos zu Hause bearbeitet werden. Anders können die Schüler*innen die vorgegebenen Zeiten nicht einhalten.
Vorbereitung
Vorüberlegungen
Diese Lerneinheit ist für die 10. Klasse konzipiert, kann aber mit Ausnahme von Lektion 4 auch schon in der 9. Klasse eingesetzt werden. Lektion 4 setzt die 10.-Klassepoche „Potenzen, Wurzeln, Logarithmen“ voraus, so dass dieses Lernmodul am effektivsten nach der genannten Epoche eingesetzt wird.
Es werden Schüler mit sehr unterschiedlichen Voraussetzungen antreten. In dieser Einheit sollten die unten genannten grundlegenden Kenntnisse beherrscht werden. Sie werden jedoch in dieser Einheit auch wiederholt.
- Ausmultiplizieren,
- Binome
- Ausklammern
- Lineare Gleichungen
In dieser Lerneinheit müssen einige Videos durchgearbeitet werden. Die Lehrperson sollte darauf achten, dass die Inhalte verstanden und nicht nur auswendig gelernt werden (was eigentlich selbstverständlich sein sollte).
Markierungen in den Aufgabenblättern
Die Aufgabenblätter enthalten folgende Markierungen:
- A die Aufgabe entspricht den Anforderungen für die Einschätzung „achieved“
- M die Aufgabe entspricht den Anforderungen für die Einschätzung „achieved with merit“
- E die Aufgabe entspricht den Anforderungen für die Einschätzung „achieved with excellence“
Außerdem werden die verschiedenen Techniken (bezogen auf die Eintragung unter LO 1025 im Handbuch) bezeichnet:
- T1: Auflösen (A, M) und Faktorisieren (M) von Klammern.
- T2: Ausklammern, Faktorisieren (nur bei A von T1 unterschieden)
- T3: Umgang mit Formeln (Einsetzen: A, Umstellen: M)
- T4: Lineare Gleichungen (A, M) und Ungleichungen (M)
- T5: Lineare Gleichungssysteme (M, E)
- T6: Quadratische Gleichungen (reinquadratische, Nullprodukt-Regel: A, Satz des Vieta, Quadratisch Ergänzen: M1)
- (T7 wird nicht benutzt)
- T8: Potenzgleichungen (A)
- T9: Exponentialgleichungen (A, M)
Vorbereitungsteil für Lektion 1
Der Vorbereitungsteil für die 1. Lektion enthält
- Fünf Videos zum Lösen von (linearen) Gleichungen. Diese Videos gehören zusammen; sie sind inhaltlich als ein einziges Video aufzufassen.
. Die Gesamtspielzeit der Videos beträgt 6:48 Minuten.
Lektion 1: Wiederholung und Vertiefung
Geplante Dauer
Richtwert: 2 Tage
Besprechnungsrunde
Das Video zeigt eine praktische Anwendung von Gleichungen. Es wiederholt die grundlegenden Regeln:
Ne(nner weg) – Kl(ammern auflösen) – O(rdnen) – Z(usammenfassen) – I(solieren).
In der ersten Besprechnungsrunde nach dem Einführungsvideo können außerdem noch grundlegende Fragen in der Lerngruppe besprochen werden.
Insbesondere muss die Lehrperson darauf achten, dass die Schüler*innen die Methoden verstanden haben. Evt. können gemeinsam Beispiele gerechnet werden.
Ablauf der Lerneinheit
Es gibt 3 Aufgabenblätter, die möglicherweise sehr schnell durchgearbeitet werden können.
- Das erste Aufgabenblatt wiederholt die wichtigsten Techniken zum Lösen von Linearen Gleichungen
- Das zweite Aufgabenblatt übt den Umgang mit Formeln (Einsetzen (A) und Umstellen (M))
- Das dritte Arbeitsblatt ist sehr kurz und enthält Aufgaben mit Ungleichungen (obligatorisch für M, T4)
Lerninhalte
- Lineare Gleichungen (Wiederholung)
- Umgang mit Formeln (Wiederholung, Vertiefung)
- Lineare Ungleichungen
Videos
- Formeln umstellen (der Weg der Theoretiker)
- Ungleichungen (5:10)
Vorbereitungsteil für Lektion 2
Der Vorbereitungsteil für die nächste Lerneinheit enthält
- Eine Wiederholung zu den Binomischen Formeln
Diese werden im nächsten Abschnitt geübt und müssen dann beim quadratischen Ergänzen angewendet werden.
Lektion 2: Quadratische Gleichungen
Geplante Dauer
4 Tage (8 Unterrichtsstunden)
Vorüberlegungen
In dieser Lerneinheit werden alle Methoden mit Ausnahme der Formel besprochen. Ziel ist es, aus dem „Algebraischen“ heraus zu arbeiten. Die Formel würde – so nützlich sie im Zusammenhang mit Prüfungen vielleicht sein mag, hier eine Abkürzung liefern, die das algebraische Verständnis nicht fördert, sondern die Schüler zu reinen „Rechenaffen“ macht.
Dieses Thema wird dann im Modul Algebra 3 wieder aufgegriffen. Dort wird dann auch die Formel erarbeitet.
Besprechungsrunde
Besprechung der Fragen auf dem Worksheet und zu den Binomischen Formeln.
Ablauf der Lerneinheit
Am Anfang drucken sich die Schüler das Aufgabenblatt aus. Zu den einzelnen Aufgabentypen gibt es extra HowTo-Anleitungen welche die Schüler zwischen durch ansehen sollen (Ohr- oder Kopfhörer verwenden, um die anderen nicht zu stören).
Die Erklärung der Methode „Quadratisch Ergänzen“ wird ganz aus dem Verständnis der Binome heraus erarbeitet: z.B.
| x² – 6x – 5 | „Die -5 ist falsch; es müsste eigentlich +9 da stehen“, also |
| x² -6x + 9 | „Um den Fehler zu beheben muss man noch 14 subtrahieren“ |
| x² -6x +9 – 14 x² -6x +9 -14 | „Jetzt kann man das 2. Binom anwenden; es bleibt jedoch ein „Rest“ von -14 übrig“ |
| ( x- 3)² – 14 |
Auch der „Satz des Vieta“ erklärt sich aus dem Algebraischen heraus, wenn man untersucht, was beim Ausmultiplizieren von 2 Klammern geschieht, kann man das Ganze rückwärts anwenden. Anschließend kommt man mit der Null-Produkt-Regel zum Ergebnis:
| (x+3)(x+5) | |
| x² +5x +3x +15 | „15 ist das Produkt aus 3 und 5“ |
| x² + 8x + 15 | „8 ist die Summe aus 3 und 5“ |
| Diesen Vorgang wird mit unterschiedlichen Rechenzeichen (+ und -) wiederholt und beobachtet, was geschieht. | |
| Jetzt kann man das Ganze rückwärts versuchen. |
Hier wird es nicht genügen nur das Video zu betrachten. Eine Bearbeitung in der Gruppe scheint mir an dieser Stelle unabdingbar zu sein.
Aufgabenblatt
das Aufgabenblatt enthält Aufgaben unterschiedlichen Schwierigkeitsgrades.
- Reinquadratische Gleichungen
- Null-Produkt-Regel
- „Satz des Vieta“
- Quadratisch Ergänzen
- Textaufgaben
HowTo-Videos
Der Lernteil enthält HowTos zu folgenden Themen:
- Reinquadratische Gleichung (2:48)
- Reinquadratische Gleichung mit Klammer (2:04)
- Null-Produkt-Regel (1:58)
- Satz des Vieta (4:57)
- Quadratisches Ergänzen (4:25)
Vorbereitungsteil für Lektion 3
Diesmal gibt es nur ein Lernvideo zum Thema
- Das Problem des Zeitungsverkäufers (1:48)
Lektion 3: Gleichungssysteme
Geplante Dauer
2 Tage (4 Stunden)
Besprechnungsrunde
Dieses Problem ist noch relativ übersichtlich und es gibt mehrere Möglichkeiten, es zu lösen. Jede Lösungsansatz und jede Idee ist willkommen. Erarbeiten der neuen Idee: Man könnte auch 2 Variable x und y benutzen…
Ablauf der Lerneinheit
Nach dem Anschauen der HowTo-Videos entscheiden sich die Schüler*innen für die ihnen sympathischere Methode und über diese mit dem Aufgabenblatt.
Vorbereitung Lektion 4
Der Vorbereitungsteil enthält ein Video zur Erkärung des 3. Keplerschen Gesetzes. Damit wird das Auflösen einer einfachen Potenzgleichung 3. Grades geübt und die nebenstehende Regel wiederholt (müsste aus der Epoche bekannt sein)
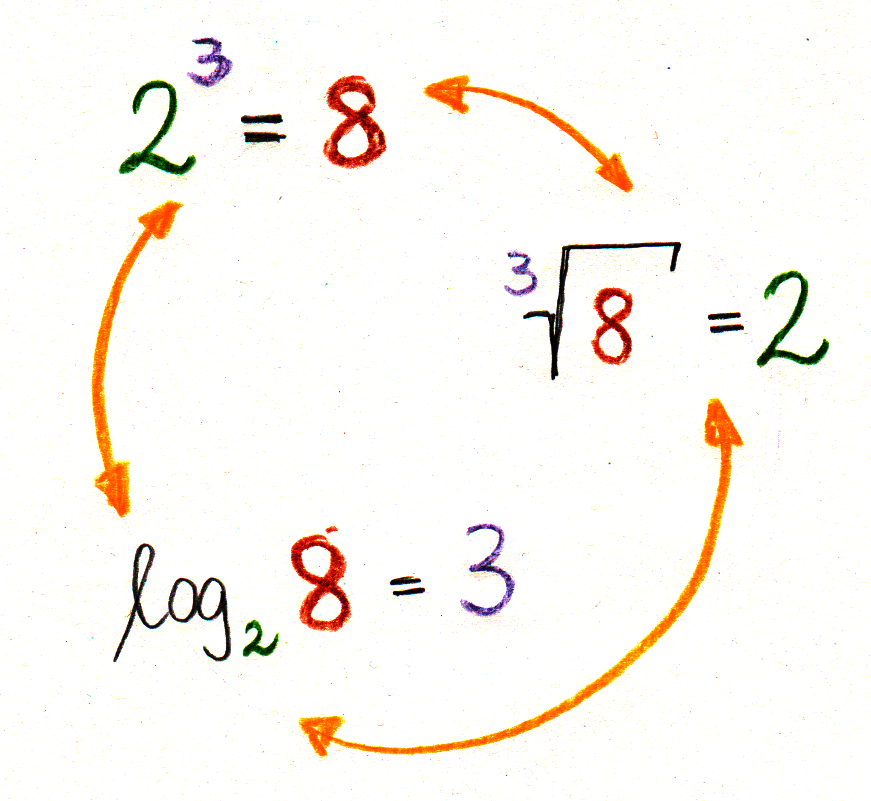
Das Worksheet enthält Fragen zu den Ellipsenbahnen.
Lektion 4: Höhere Gleichungen
Geplante Dauer
1 Tag (2 Stunden)
Vorüberlegungen
Um die Lerneinheit nicht allzu sehr in die Länge zu ziehen, wird auf das Ermitteln der Definitionsmenge keinen Wert gelegt. Dies ist insofern berechtigt, als beim Durchführen der obligatorischen Probe nicht zulässige Werte sowieso herausfallen.


